WolframAlphaの使用例(1)
http://bit.ly/s0u8D1 WolframAlpha.\int_0^{\pi/2}\sin x/(1+\cos x)dx と入力すれば定積分が計算される。Jacobi theta functions と入力すると詳しい説明へのリンクが出て来る。公式集いらずになる。
WolframAlpha http://bit.ly/wzyqLT のように極限の計算もできる。 http://bit.ly/w9AHEl のように行列のランクも計算できる。 http://bit.ly/xACgu9 のようにして固有値固有ベクトルも計算できる。
WolframAlpha http://bit.ly/s0u8D1 で行列の入力の仕方を知りたければ matrix を検索 http://bit.ly/wGysHZ すればよい。ぼくはスマホにWolframAlphaのアプリを入れている。ブラウザよりも入力が楽になる。
WolframAlpha http://bit.ly/s0u8D1 試験で行列の対角化の問題を必ず出すと言ってある。これ使われちゃうと本当に困る。ややこしい数式処理を使える学生であれば試験も普通に楽勝だと思うが、WolframAlphaは5分で使い方をマスターできる。
5 Forbidden Back to School Apps http://www.youtube.com/watch?v=Bb74xMU7dUA … で WolframAlpha が紹介されていた。
全然別の話。「数学の試験問題をスマホを使って解く」ということに関しては http://www.wolframalpha.com/ のスマホアプリ(有料)がとても便利です。数式処理ソフトと違って適当に入力すれば適当な答えが返って来る。

続き。たとえば某試験問題の1番の行列Aについてはこんな感じ。WolframAlphaへの入力は {{0,1,√2},{1,√2,1},{√2,1,0}} だけ。結果は添付画像の通り。pic.twitter.com/pbmXxvnOCv
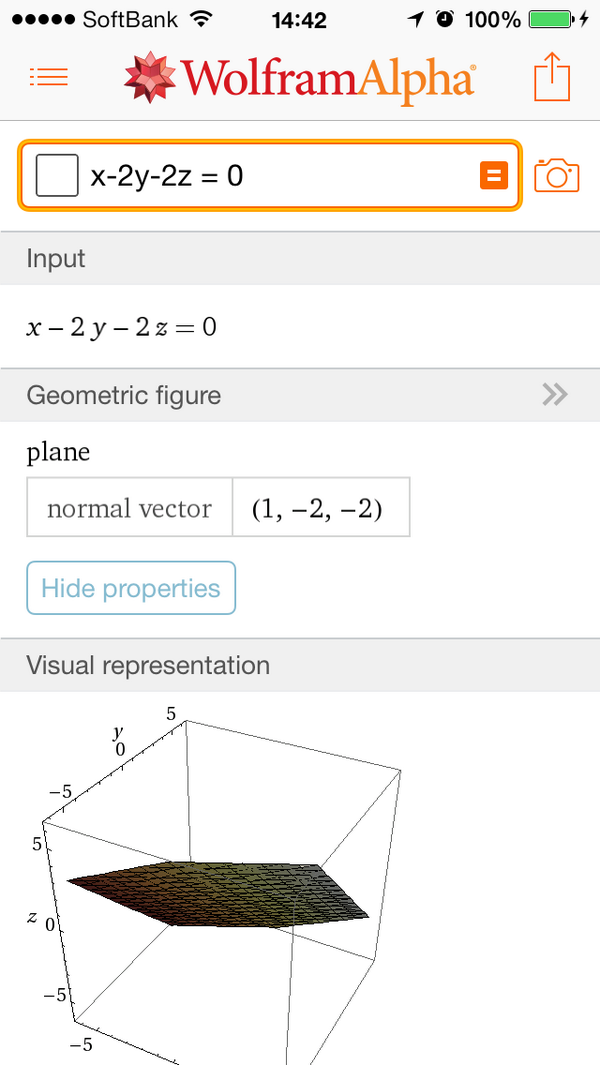
続き。問題3番についてはこんな感じ。ポイントはまじめに数式処理のための入力をしなくても、適当に関連の式情報を入力すればその式関連の情報を色々教えてくれること。pic.twitter.com/2o2dodtx29
続き。WolframAlphaですが、微積分の計算問題も非常によくやってくれます。気楽に入力できるので数式処理ソフトよりも気軽に使えて便利です。(実は自分で作った試験問題のチェックに結構使っていることは秘密だ。)

穴があったら入りたい気持ち ".@genkuroki 某試験問題の1番の行列Aについてはこんな感じ。WolframAlphaへの入力は {{0,1,√2},{1,√2,1},{√2,1,0}} だけ。結果は添付画像の通り。 pic.twitter.com/5PpA0nvjcJ"
@Paul_Painleve ぼくが出した問題にはある具体的に与えられた2変数函数のグラフが(x,y)=(0,0)の近くでおわん型、馬のくら型、ひっくり返ったおわん型のどれになるかという問題があるのですが、WolframAlphaはグラフも表示しちゃうので瞬殺されちゃいます。
@genkuroki もう、今後はそれはそれで正解でも良いような気が…と世間に負けつつあります。2変数多項式程度でも、グラフ見てるだけだとわかりにくい例もあったような記憶がありますので、そういう例を出していくしかないのかもしれません。
テキストで数式x^a で「xの右上に小さなa」の意味(xのa乗)。x_a で「xの右下に小さなa」の意味。たとえば ∫_0^1 x^{n-1} dx = 1/n は「xのn-1乗をxで0から1まで積分すると1/nになる」という意味。^ と _ をぼくはよく使っている。
続き。WolframAlpha に ∫_0^1 x^{n-1} dx と入力するとしっかり計算してくれる。http://tinyurl.com/qj3lpp5 WolframAlphaは∫∞√などの記号を適切に解釈してくれる。1+x^2の平方根は√{1+x^2}と書くと誤解が減る。
大学新入生へのおすすめ有料アプリ。それはWolfram Alphaのアプリ。http://products.wolframalpha.com/mobile/ ブラウザで https://www.wolframalpha.com/ にアクセスすれば無料でも使えるが、スマホにアプリを入れておくととても便利。続く
たとえば http://goo.gl/iRWKfr のようにint_{-infty}^infty exp(-x^2) dxとTeXっぽく数式を入力すれば答えを教えてくれます。数式処理ソフトと違って入力がてきとーでよい点がとてもありがたい。続く
Wolfram Alpha 関係リンク集使い方を検索https://www.google.co.jp/search?num=100&hl=ja&q=Wolfram+Alpha+使い方 …計算サービス「Wolfram|Alpha」の使い方http://matome.naver.jp/odai/2139782055327564601 …
行列を {{1,2},{3,4}} のように入力するとその行列関係の主要な「不変量」をリストアップして教えてくれます。 http://goo.gl/Bi9uLR これを知っていれば大学1年生レベルの線形代数の試験問題の7割程度は答えを簡単に得ることができます。
Wolfram Alphaの素晴らしいところは、数式処理ソフトの文法に沿って「正しい入力」をしなくても、てきとーに入力するだけで有益な情報を返してくれることです。これは本当におすすめ。ぼくもよく使っています。
http://goo.gl/j8gltk Wolpram Alpha https://www.wolframalpha.com でz=x^2y/(x^2+y^2)と入力すれば「原点で偏微分可能だが微分不可能な函数」のグラフを簡単に見ることができます。百聞は一見に如かず。
数学こねた。(x)_q=(1-q^x)/(1-q)とおく。これはq→1でxに収束する。xが数であるとき(x)_qはq-numberと呼ばれることがある。q数は普通の数のパラメータqによる変形とみなせる。q数は普通の数が満たしている多くの性質を満たしている。続く
高校レベルのこネタ続き。(x+1)_q-(x)_q=q^x=e^{xh}=Σ x^n h^n/n! なので、f_n(x+1)-f_n(x)=x^n である。 f_n(0)=0だったので、正の整数kに対して、~続く
続き~、n>0のとき、f_n(k+1)=f_n(k)+k^n=f_n(k-1)+(k-1)^n+k^n=…=f_n(0)+0^n+1^n+…+(k-1)^n+k^n なのでf_n(k+1)=1^n+2^n+…+k^nとなる。まとめに続く
続き。要するに、q=e^hとおくとき、q数 (k+1)_q = (1-q^{k+1})/(1-q) のhに関する展開の h^n/n! (n>0)の係数は1からkまでのn乗の和になっている。q数は実はべき乗和の母函数であった。細かいところをミスっていたらごめん。続く
続き。実は最初からx=k+1 (kは正の整数)とおいておけば、(k+1)_q=(1-q^{k+1})/(1-q)=1+q+…+q^kであり、q^j = e^{jh} = Σ j^n h^n/n! なので (k+1)_q が j^n の和の母函数であることは最初から明らか。
続きのおまけ。よくある解説では、ベルヌイ数を母函数を使って定義して、ベルヌイ数を使ってn乗和を表わせることを証明しています(結構複雑)。そのスタイルと以上のq数を単純に母函数とみなす話を比較すると、q数の定義式の一部分にベルヌイ数の母函数が見えていることもわかります。
続きの細かい話。q数を単純に母函数とみなすとh^0の係数がxになって、xにk+1を代入するとk+1になり、1からkまでの0乗の和になりません。これをどうにかできないでしょうか?さらにxにk+1ではなく、kを代入して1からkまでのn乗和が出て来るようにできないでしょうか?続く
続き。そこをうまく処理するためには (x)_q をそのまま母函数とみなさずに、それに q をかけた q(x)_q = q(1-x^)/(1-q) を母函数とみなすとよいです。なぜならば正の整数kに対して q(k)_q = q+q^2+…+q^k だからです。
続き。正の整数kについて、q(x)_q=q(1-q^x)/(1-q)のhに関する展開のh^n/n!の係数は1からkまでのn乗和になります。よくある解説のベルヌイ多項式の母函数はB(x,h)=-hq^x/(1-q)で、q(x)_q=(B(x+1,h)-B(1,h))/hです。続く
続き。ベルヌイ多項式B_n(x)はB(x,h)=-hq^x/(1-q)のhに関する展開のh^n/n!の係数として定義されるので、等式q(x)_q=(B(x+1)-B(1,h))/hの両辺の展開を比較すればn乗和をベルヌイ多項式で表わす公式も得られます。
https://twitter.com/genkuroki/status/609194308378345472 … の誤植。 「 q(x)_q = q(1-x^)/(1-q) 」は誤りで、正しくは「 q(x)_q = q(1-q^x)/(1-q) 」です。q^x は e^{xh} の便利な略記だと思っておくとよいです。
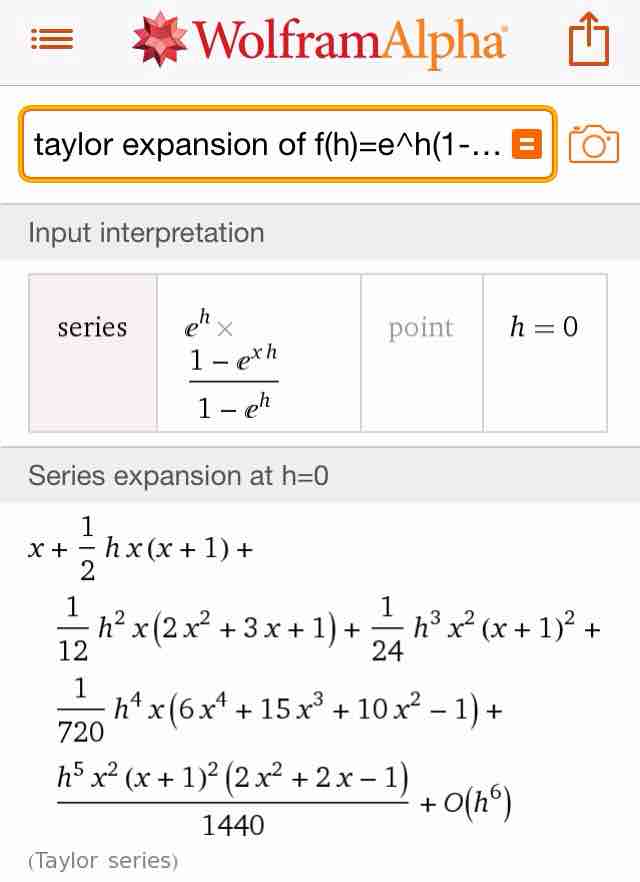
@genkuroki 高校レベルの小ネタ続き。反応がないので、スマホのWolframAlphaアプリによるTaylor expansion of f(h)=e^h(1-e^{xh})/(1-e^h) at h=0の計算結果を貼り付け。pic.twitter.com/FxF3UBzKua
@sekibunnteisuu 一般に(x)_q=(q^x-1)/(q-1)をq-numberと呼びます。数xのパラメーターqによる一般化。q→1で普通の数に戻る。q-numberのままで普通の数と同様の公式がたくさん成立しています。続く@spiral_world
@sekibunnteisuu q(n)_q=q+q^2+…+q^nなので、q=exp(x), f_n(x)=q(n)_qとおくとf_n^{(k)}(0)=1^k+n^k+…+n^k (k乗和)http://www.wolframalpha.com/input/?i=series+of+f(x)=exp(x)(1-exp(nx))/(1-exp(x)) …@spiral_world
@genkuroki @sekibunnteisuu @spiral_world 「等比数列q,q^2,...,q^nの和」= 「q数 q (n)_q」は「1からnまでのすべてのk乗和の情報」を持っています。全部高校数学の範囲内の話。
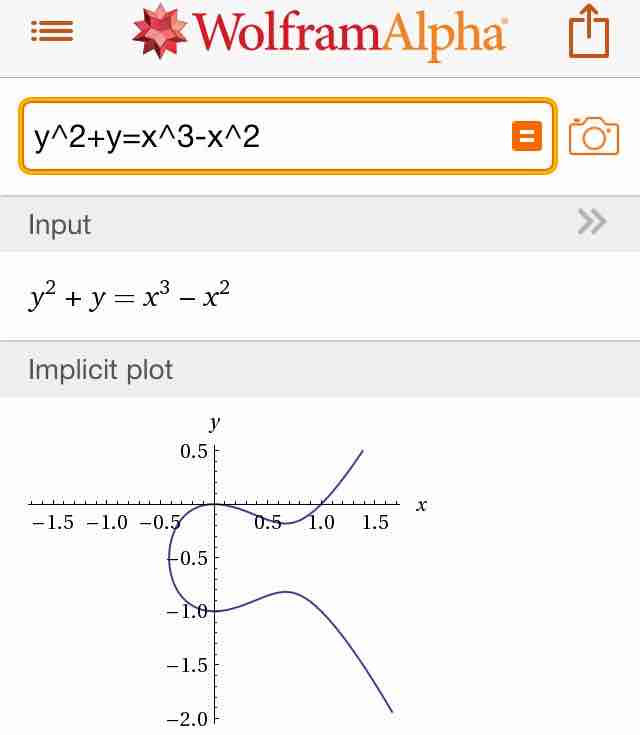
@genkuroki #数楽 添付画像はx,yに関する3次方程式y^2+y=x^3-x^2で定義される楕円曲線を実平面でプロットしたものです。方程式の解を実数の範囲内で求めてグラフを描いたものです。pic.twitter.com/G6GxYABecU
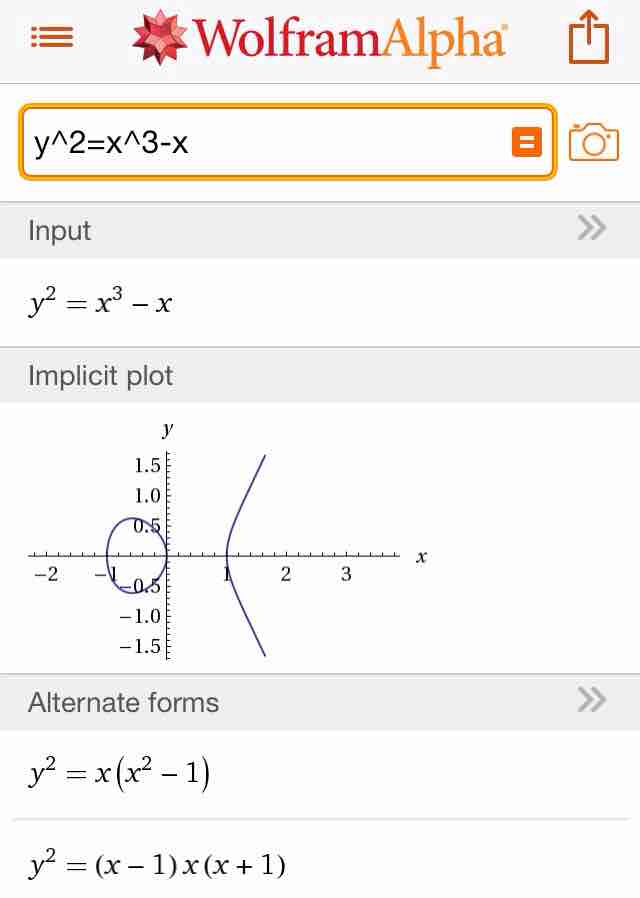
@genkuroki #数楽 添付画像は別の楕円曲線y^2=x^3-xの実平面でのグラフです。こういうときにWolframAlphaはとても便利です。pic.twitter.com/J2HuymOpvw
@genkuroki #数楽 楕円曲線の数学に関して大事なことの一つはx,yに関する3次方程式の解を探す範囲を実数に制限する必要がないことです。例えば複素数や有限体の中に解を探してもよい。複素数の中で解を探すと、楕円曲線は巨大なトーラス状の実曲面になっていることがわかります。

@genkuroki #数楽 pic.twitter.com/J2HuymOpvw添付画像は実数の範囲内で楕円曲線をプロットしたものです。複素数まで範囲を広げると巨大なトーラス状の曲面になっているのですが、その実平面による断面が見えていることがわかります。

@genkuroki #数楽 pic.twitter.com/J2HuymOpvwグラフの卵型の部分はトーラスを切って出る輪っかの一つです。右側の広がっている部分も実は無限遠(射影平面上で考える)で上下が繋がっていて輪っかになっています。トーラスの断面(輪っかが2つ)が見えている。
@genkuroki #数楽 実平面による切断面を眺めるだけではなかなか納得できないことですが、複素数の扱いを学ぶと、楕円曲線を定義するx,yに関する3次方程式を複素数の範囲内で解いて「プロット」して無限遠点を付け加えるとトーラスになることがわかります。
.@genkuroki #数楽 続き。そういうわけで便利な電卓サイトを探してみたのですが、私の結論は「WolframAlphaを使いましょう」です→ http://wolframalpha.com 。任意精度計算も modulo 計算も容易です。続く
@genkuroki #数楽 たとえば5 digits of 1/131→1/131を有効桁5桁で計算10^65 mod 131→10の65乗を131で割った余り1/131の66桁目を知りたければ→67 digits of 1/131+0.1→終わりから2番目の数字
@genkuroki #数楽 http://www.wolframalpha.com/input/?i=Is 2^6972593-1 prime? …WolframAlphaは「2^6972593-1は素数」と答えてくれました。超巨大素数の表も持っているのかな?
@genkuroki #数楽 ウェブブラウザ以外に使える道具がなくても、WolframAlphaにアクセスすれば遊ぶために必要な計算は全部できます→https://twitter.com/genkuroki/status/705716359313817601 …
@genkuroki #数楽 WolframAlphaでは10進小数点展開だけではなく、5進小数展開の類も計算できますね。http://www.wolframalpha.com/input/?i=1/59 to base 5 …パターンを見つけたければ素数分の1の5進小数展開を調べた方がよいかも。
@genkuroki #数楽 いや、素数分の1の2進小数展開のパターン探しも手頃で楽しいかも。http://www.wolframalpha.com/input/?i=1/19 to binary …
#数楽 Nemesさんによるスターリングの公式のコンパクトな改良n!≒(n+1/(12n-1/(10n)))^ne^{-n}√(2πn)もあります(Nemesの公式)。NemesさんによるLaplaceの方法の詳しい解説はすでに引用してあります。
#数楽http://www.wolframalpha.com/input/?i=n=1,+((n+1/(12n-1/(10n)))/e)**n√(2πn),+n …!Stirling-Nemesの公式をn=1で計算
#数楽 http://www.ebyte.it/library/downloads/2007_MTH_Nemes_GammaFunction.pdf …Nemesさんによるn!の階乗の様々な近似式の比較。ここにNemesの公式も書いてある。インターネット時代になって数学ネタでは多くの場合原論文を誰でも見られるようになりましたね。論文を公開していない分野は遅れを取ると思う。
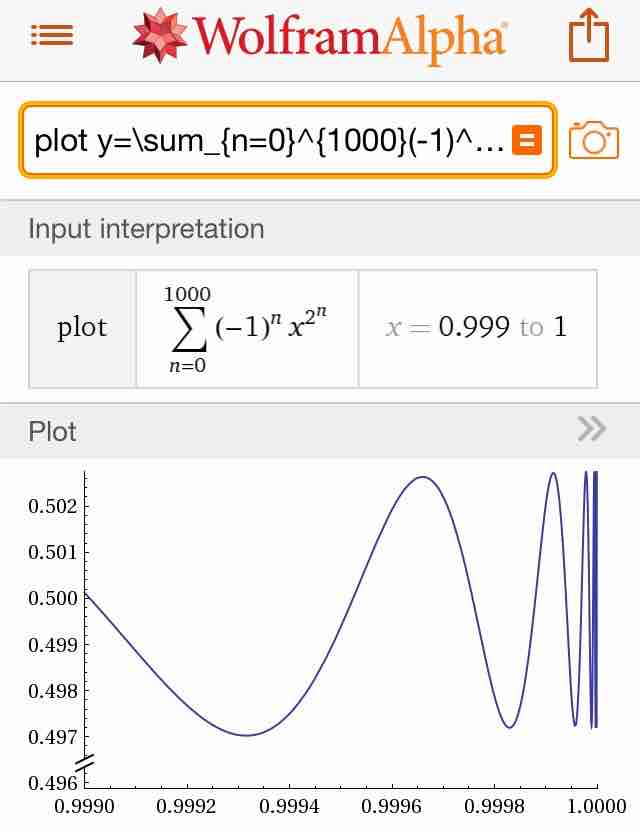
#数楽 WolframAlphaで x-x^2+x^4-x^8+x^{16}-…の0.999<x<1のでのグラフを書いてみた。確かに無限に振動しているっぽいよね(実際している)。pic.twitter.com/ESzdYarf17
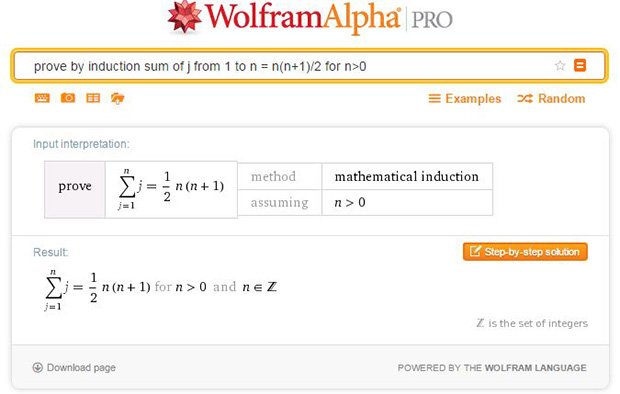
Wolfram|Alphaで数学的帰納法を使った証明ができるようになりました。世界初です!ブログをご覧ください。 #wolframalpha http://wolfr.am/edDrzAXF pic.twitter.com/GBTCk2FhY5
#東北大学オープンキャンパス#数学http://wolframalpha.com WolframAlphaはとても便利。素数大富豪での素数判定に使えるだけではなく、かなり難しい計算もしてくれます。公式集を持ち歩く必要がかなり減る感じ。
私個人はiPhoneに有料のWolframAlphaのアプリを入れて計算時間の制限を外して使っています。相当に便利です。おすすめ!
たとえば、ζ(2)=Σ_{n=1}^∞ 1/n^2 の積分表示をWolframAlphaで計算→ http://www.wolframalpha.com/input/?i= %E2��_0**1(∫_0**x 1/(x(1-y)) dy)dx …
WolframAlphaは、大学数学科学部レベルの積分はうまく入力すれば大抵計算してくれる。「ツイッターでURLを引用し易くするためには、^の代わりに**を使えばよい」と覚えておくと便利です。先の例→ http://www.wolframalpha.com/input/?i= %E2��_0**1(∫_0**x 1/(x(1-y)) dy)dx …



